Alan Turing, sur les traces de l’IA : Episode 8 – la machine de Turing, première partie
Nous allons essayer de centrer cet épisode de notre « saga » sur Turing sur un de ses articles, qui a connu une fortune importante dans le vingtième siècle , à savoir « Théorie des nombres calculables, suivie d’une application au problème de la décision ». Nous le ferons en deux temps.
Rappelons encore une fois que 2012 sera l’année anniversaire de la naissance de Turing. Et j’invite donc ceux qui ne le connaissent pas encore à lire les premiers articles que j’ai postés sur sa vie :
Alan Mathison Turing, sur les traces de l’Intelligence Artificielle : Introduction
Beaucoup d’hommages auront assurément lieu. Citons par exemple celui-ci, car il concerne un autre domaine qui m’importe, à savoir la place grandissante des machines et des robots dans nos vies :
Un robot pourrait porter la flamme olympique
Ainsi donc, cet article de Turing, écrit en 1936, « Théorie des nombres calculables, suivie d’une application au problème de la décision », s’inscrit dans les travaux de recherches sur la théorie des fonctions calculables, et plus largement comme nous l’avons vu, dans les recherches autour du programme de Hilbert. Encore une fois, je ne pourrai entrer dans les détails des démonstrations de Turing du fait de mes propres limitations et lacunes en Mathématiques.
Pour lire l’article en anglais : ON COMPUTABLE NUMBERS, WITH AN APPLICATION TO THE ENTSCHEIDUNGSPROBLEM
Nous avions vu que Turing s’était intéressé à la physique et surtout à la chimie. Des disciplines où la notion de déterminisme est importante.
La psychanalyste Christiane Alberti nous rappelle dans un article très intéressant « Alan Turing et sa A-machine : le moment de la logique » que Turing s’était senti porter vers « un questionnement sur la cohérence logique de la théorie mais aussi sur la signification de la notion de vérité absolue. »[1] Nous avions effectivement vu avec son biographe Hodges que Turing avait découvert en 1933 avec grand intérêt les écrits de John von Neumann sur la mécanique quantique (Les fondements mathématiques de la mécanique quantique). Il avait probablement déjà lu également les ouvrages de Schrödinger et de Heisenberg. Et il semble que l’intérêt de Turing ait été stimulé durant cette période par le fait que von Neumann « travaillait sur la cohérence logique de la théorie et non sur ses résultats expérimentaux. » La même année, Turing avait également lu l’ouvrage de Russel, Introduction à la philosophie mathématique. Cela lui avait permis d’approcher le problème de la signification de la vérité, à partir du moment où « les mathématiques devaient être considérés comme un jeu soumis à des règles arbitraires dans le maniement de ses symboles […] »[2].
On peut rapprocher la question du déterminisme en mathématiques du problème dit de la décidabilité dans un système formel (un système tel que l’arithmétique de Peano). Ce problème peut s’énoncer comme le fait d’être capable de savoir si telle assertion (tel théorème) ou sa négation peuvent être démontrées (ou encore dérivées) au sein de ce système formel. S’inscrivant dans le programme de Hilbert, et au courant des résultats de Gödel via les enseignements du mathématicien Newman, Turing va finalement réussir avec à sa découverte, à « abstraire cette qualité d’être déterminé pour l’appliquer à la manipulation de symboles. »
Retour sur Gödel…
Dans l’épisode précédent, j’ai cherché à montrer comment le problème de Hilbert concernant la décision (le fameux dixième problème de Hilbert en 1900, qui concernait la décision des équations diophantiennes) pouvait être compris comme la recherche d’un algorithme. J’ai également cherché à montrer comment ce problème de la décision s’était articulé au problème dit de la calculabilité, tout d’abord avec les résultats de Gödel.
Avec Gödel, on peut énoncer que si un système formel (tel qu’il serait capable de formaliser l’arithmétique des entiers, comme celui de Peano donc) est cohérent ou consistant (autrement dit, sans contradiction), alors il existe au moins un énoncé dans ce système tel qu’il n’est pas possible de le dériver dans ce système. Le système est donc dit incomplet. Il y existe un reste qui échappe à la démonstration au sein de ce système formel.
Puis, l’on peut également dire que si ce système formel (toujours comme celui de l’arithmétique de Peano) est cohérent (c’est-à-dire encore une fois, que l’on ne peut y démontrer une proposition P et sa négation non-P), et que si l’on y applique le premier résultat, à savoir qu’il existe au moins une proposition impossible à démontrer (c’est-à-dire à dériver des axiomes) alors la proposition au sein de ce système formel qui démontrerait la cohérence de ce dernier est impossible à dériver au sein de ce même système.
« Grossièrement, le théorème d’incomplétude affirme que tout langage consistant, susceptible d’être compris par une machine et suffisamment riche pour exprimer les nombres entiers avec les opérations d’addition et de multiplication, permet de formuler des propositions indécidables, qui ne sont ni démontrables, ni réfutables dans ce langage, des propositions que l’on sait devoir être vraies bien que l’on ne puisse pas les démontrer dans ce langage. De ce premier théorème, on déduit qu’il est impossible d’établir la consistance, la non-contradiction, d’un tel langage au moyen de raisonnements qui pourraient s’exprimer dans ce langage. »[3]
En d’autres termes, il n’est pas possible de démontrer la complétude d’un système formel consistant, à l’intérieur de ce même système. Et en vertu de ce résultat, il n’est pas possible de prouver, toujours à l’intérieur de ce même système formel consistant, sa propre consistance. Par exemple, au sein de ce système formel qu’est l’arithmétique de Peano, il n’est pas possible de déduire syntaxiquement des axiomes posés au départ (c’est-à-dire de dériver simplement de ces axiomes) l’ensemble des propositions vraies.
Pour arriver à ses fins, Gödel s’est proposé d’« arithmétiser la syntaxe ». C’est un point important de la démonstration de Gödel, et Turing va emprunter cette même démarche. Gödel se propose en effet de coder les formules du système formel sur lequel il effectue sa démonstration. « L’idée maîtresse, dans la démonstration de Gödel, est de représenter par des formules arithmétiques les propriétés métamathématiques, qui ont pour objets des formules arithmétiques. »[4]
« Il ne faut pas se méprendre sur le sens de ce résultat imposant de l’analyse de Gödel : il n’exclut pas la possibilité d’une démonstration métamathématique de la consistance de l’arithmétique. Ce qu’il exclut, c’est la possibilité de refléter cette démonstration dans les déductions formelles de l’arithmétique. »[5] Ce qui n’est pas la même chose… Ce à quoi le théorème de Gödel invite en effet, c’est à produire de nouveaux principes de démonstration étant donné que « l’on ne peut pas axiomatiser entièrement les ressources de l’intelligence humaine […] Les propositions mathématiques qui ne peuvent être établies par une déduction formelle à partir d’un ensemble donné d’axiomes peuvent l’être néanmoins par un raisonnement métamathématique non formalisé.»[6]
Rappelons que le mathématicien Alonzo Church (1903 – 1995), qui a beaucoup œuvré également concernant les bases théoriques de l’informatique, proposa une thèse (c’est-à-dire qu’il n’a pas totalement prouvé le résultat) quasiment au même moment où Turing parlait de sa découverte à Newman ; thèse que l’on appelle parfois Thèse de Church-Turing (car c’est seulement avec le concept de machine de Turing que le concept de mécanique prend véritablement sens) et qui pose l’équation « calculable = récursif »[7]. Mais la notion de fonction récursive n’est pas simple à manier. Et c’est pourquoi elle n’aura pas la postérité des machines de Turing.
Lecture de l’article de Turing
Afin d’avancer sur une définition de la notion de calcul, Turing donne d’emblée, dès le début de son article, une définition de ce qu’est selon lui un nombre calculable : « On peut définir sommairement les nombres ‘calculables’ comme étant les réels dont l’expression décimale est calculable avec des moyens finis. […] Selon ma définition, un nombre est calculable si sa représentation décimale peut être décrite par une machine. »[8] Et il différencie les « nombres définissables » des « nombres calculables ». Selon Lassègue, « L’étude des nombres réels pour la délimitation de ce qui est accessible au calcul s’impose donc puisque l’on est assuré a priori que certains nombres réels y échapperont toujours : c’est donc au sein de cet ensemble de nombres qu’il sera le plus facile de tracer des limites à la calculabilité. »[9]
En fonction de cette première définition, Turing va introduire dans son article sa notion de machine à calculer, via l’analogie suivante : « Un homme en train de calculer la valeur d’un nombre réel peut être comparé à une machine susceptible de se trouver dans un nombre fini d’états q1, q2, …, qR, que nous appellerons ses m-configurations ». C’est un point extrêmement important car Turing imagine donc ici que l’esprit humain peut être décrit dans les termes d’une machine. Cela n’est pas rien. Il fait appel à l’imaginaire de son époque.
Qu’est-ce que cela veut dire ? D’une part, que Turing commence par nous emmener finalement assez loin d’une démonstration logique. Il le dit lui-même. Il pose d’emblée sa thèse et l’analogie censée la démontrer, et dit ensuite qu’il va détailler le fonctionnement de ses machines pour défendre son point de vue sur ce qu’est un nombre calculable. Il reprendra son analogie calculateur humain un peu plus loin dans son article comme on va le voir.
Comme le dit ailleurs Pierre Cassou-Noguès dans son « histoire de machines, de vampires et de fous », l’article de Turing finit par nous donner une définition de la calculabilité comme « résultat logique fondé dans l’imaginaire. »[10] Qu’est-ce qu’une machine finalement ? C’est un dispositif avec deux propriétés principales : 1) une machine n’a effectivement qu’un nombre fini d’états qui lui sont propres. Et c’est pourquoi la machine de Turing est équivalente à la table de fonctionnement de la dite machine. 2) ce qu’effectue la machine à l’instant T, ne dépend que de l’état de la machine à l’instant T (son qR dans les termes de Turing) et des données qui lui parviennent via un dispositif quelconque. (Dans la machine de Turing, inspiré de la machine à écrire comme on le verra plus loin, ce sera le ruban découpé en cases contenant des symboles à déchiffrer. Dans le cas d’un ordinateur, ce sera un humain qui tape sur son clavier. On peut remarquer qu’une horloge est également une machine, mais qu’elle ne reçoit pas d’information de l’extérieur, son fonctionnement est donc entièrement déterminé par son état à l’instant T).
Aussi, dire qu’un homme en train de calculer, un calculateur humain, peut être comparé à une machine suppose que les différents états mentaux de l’esprit humain soient en nombre fini d’une part. Et d’autre part, cela suppose que cet homme n’agit qu’en fonction de son état mental à l’instant T, associé aux données extérieures qui lui parviennent par ses sens, et suppose enfin qu’il agira toujours de la même façon s’il se trouve dans tel état qR, avec les mêmes données extérieures.
Qu’un corps, ou plutôt, qu’un organisme biologique soit réductible à la notion de machine, il est possible de le concevoir. Mais concevoir que les différents états mentaux soient en nombre finis n’est pas si aisé il me semble, en raison même de l’expérience que nous avons de notre propre esprit, qui nous pousserait plutôt à concevoir celui-ci comme une expérience du continu. Enfin de quelle nature sont ces états mentaux, c’est encore une autre grande question…
Et pourtant, cette analogie nous paraît plausible d’un point de vue imaginaire. Elle fonctionne même plutôt pas mal…
Dans cette perspective, imaginaire, il serait possible à chaque instant de déterminer dans quel état (parmi un certain nombre déterminé et fini), dans quelle configuration se trouve la machine mentale. « Le couple (qn, S(r)) est appelé la configuration de la machine, et c’est donc cette configuration qui détermine l’évolution possible de la machine […] »[11] où qn désigne pour Turing l’état de sa machine à l’instant T, et S(r) le symbole inspecté par la tête de lecture de sa machine.
De la machine à écrire à la machine de Turing
Turing s’inspire de la machine à écrire, qui manipule aussi des symboles. « Qu’est-ce qui faisait qu’une machine à écrire était ‘mécanique’ ? Cela était lié au fait qu’à une action de l’opérateur correspondait de façon certaine une réponse de la machine dont on pouvait décrire à l’avance le comportement dans tous les cas de figure. […] la réponse dépendra de l’état en cours de la machine, de sa ‘configuration’, dira Alan, pensant aux positions majuscule et minuscule ; une idée qu’il reprit sous une forme plus générale.»[12]
Le modèle de la machine à écrire apparaît cependant trop limité, notamment à cause du fait que la machine à écrire ne peut qu’écrire et non lire des symboles. Sa machine doit être capable d’écrire (write), mais aussi de lire (d’inspecter dans ses termes : scan), d’effacer (delete), et enfin de se déplacer à gauche ou à droite.
Turing reprend ainsi du fonctionnement de la machine à écrire le fait que sur cette dernière on ne peut effectuer qu’un nombre fini d’opérations, et que l’on peut dresser « un compte rendu détaillé et définitif du comportement intégral de la machine. »[13] Autre élément important, sa machine reprend l’idée du déplacement du point de frappe sur la page. Il simplifia ce point en imaginant « des machines n’opérant que sur une seule ligne d’écriture. […] Dans son idée, le point de frappe de sa super-machine à écrire pouvait se déplacer indéfiniment vers la gauche ou la droite. »[14] Le ruban de papier, support de cette ligne d’écriture, sera pensé comme infini, mais également divisé en cases. On peut également imaginer que ce soit le ruban qui se déplace et non la tête d’écriture/lecture.
A chaque étape, son fonctionnement est donc déterminé par sa configuration du moment, son état, ainsi que par le symbole déchiffré, lu, par la tête de lecture de la machine. C’est ce qu’il appelle le couple (qn, S(r)), encore appelé la configuration de la machine. Une table de fonctionnement peut être écrite, qui définira complétement la machine. « D’un point de vue abstrait, la table était la machine elle-même. »[15]
L’idée est donc que sa machine doit être entièrement automatisée, sans qu’un opérateur n’ait à agir ou prendre de décision, et qu’elle devait être en mesure de déchiffrer « toute assertion mathématique qui lui serait présentée pour juger si elle était démontrable ou non. Mais il fallait impérativement que ce verdict soit rendu sans la moindre interférence avec l’intelligence, l’imagination ou le jugement humains. »[16]
Cette machine doit donc être capable de faire des additions, des multiplications, d’être finalement capable de savoir, ou plutôt de décider par exemple (c’est-à-dire de dérouler un algorithme comme on l’a vu précédemment) si un nombre est divisible par un autre, ou encore si un nombre est premier.
Les élements importants de la machine
On a donc :
- Un ruban « avec une extrémité gauche, infini à droite, divisé en cases de même taille […] »[17]
- Un ensemble fini de symboles, qui vont servir à la description et au fonctionnement de la machine. Ils seront imprimés sur le ruban.
- Le ruban, qui sera donc la mémoire. Il permet de stocker temporairement les symboles, car il permet l’écriture et la lecture.
- La tête de lecture/écriture. Elle peut rester sur place, ou se déplacer vers la gauche ou la droite. Enfin, elle peut lire ou écrire un symbole dans une case du ruban.
- Un ensemble fini d’états sachant que « ces états permettent de distinguer plusieurs comportements possibles […] »[18]
- « Un ensemble fini d’instructions : à chaque étape, en fonction du symbole c que la tête lit dans la case sondée et en fonction de son état courant S, elle écrit un nouveau symbole c’ […], elle passe dans un nouvel état S’ […] et elle effectue un déplacement […] »[19]
L’idée est qu’avec cette machine, on puisse normalement simuler n’importe quel algorithme.
Mais comment ce type de machine, décrite par une table quelconque, est censé finalement résoudre le fameux problème de décidabilité d’Hilbert ?
Après avoir présenté brièvement sa machine à calculer, Turing va affirmer que les opérations que peut effectuer sa machine « englobent toutes celles qui peuvent être utilisées pour calculer la valeur d’un nombre. »[20] Et il propose ensuite de présenter sa « théorie des machines » afin de défendre ce point de vue. Son article est ainsi écrit d’une manière plutôt originale pour un article théorique en mathématique.
Nous terminerons sa lecture au prochaine épisode.
La machine de Turing est un concept. Ce n’est donc en rien le plan d’une machine concrète. Voici cependant une vidéo qui me paraît donner une figuration du concept de « machine de Turing » que vous pouvez regarder ici :
Vidéo d’une « machine de Turing«
[1] Christiane Alberti, « Alan Turing et sa A-machine : le moment de la logique », in Le traumatisme de la langue – études cliniques, Association Himeros, 2007, p. 62
[2] Andrew Hodges, Alan Turing ou l’énigme de l’intelligence, Payot, 1983, 1988, p. 77.
[3] Pierre Cassou-Noguès, Gödel, Les Belles Lettres, 2008, p.60
[4] Pierre Cassou-Noguès, Gödel, Les Belles Lettres, 2008, p.62
[5] Ernest Nagel, James N. Newman, « La démonstration de Gödel », in Le théorème de Gödel, p. 91
[6] Ernest Nagel, James N. Newman, « La démonstration de Gödel », in Le théorème de Gödel, p. 94
[7] Jean-Yves Girard, « La machine de Turing : de la calculabilité à la complexité », in La machine de Turing, Alan Turing, Jean-Yves Girard, Seuil, 1995, p. 13.
[8] Alan Turing, « Théorie des nombres calculables, suivie d’une application au problème de la décision », in La machine de Turing, Alan Turing, Jean-Yves Girard, Seuil, 1995, p. 49
[9] Jean Lassègue, Turing, Les Belles Lettres, 1998, p. 71
[10] Pierre Cassou-Noguès, Une histoire de machines, de vampires et de fous, Vrin, 2007, p.160
[11] Alan Turing, « Théorie des nombres calculables, suivie d’une application au problème de la décision », in La machine de Turing, Alan Turing, Jean-Yves Girard, Seuil, 1995, p. 51
[12] Andrew Hodges, Alan Turing ou l’énigme de l’intelligence, Payot, 1983, 1988, p. 91.
[13] Andrew Hodges, Alan Turing ou l’énigme de l’intelligence, Payot, 1983, 1988, p. 91.
[14] Andrew Hodges, Alan Turing ou l’énigme de l’intelligence, Payot, 1983, 1988, p. 91.
[15] Andrew Hodges, Alan Turing ou l’énigme de l’intelligence, Payot, 1983, 1988, p. 92.
[16] Andrew Hodges, Alan Turing ou l’énigme de l’intelligence, Payot, 1983, 1988, p. 92.
[17] Jean-Yves Girard, « La machine de Turing : de la calculabilité à la complexité », in La machine de Turing, Alan Turing, Jean-Yves Girard, Seuil, 1995, p. 31.
[18] Jean-Yves Girard, « La machine de Turing : de la calculabilité à la complexité », in La machine de Turing, Alan Turing, Jean-Yves Girard, Seuil, 1995, p. 31
[19] Jean-Yves Girard, « La machine de Turing : de la calculabilité à la complexité », in La machine de Turing, Alan Turing, Jean-Yves Girard, Seuil, 1995, p. 31 et p.32
[20] Alan Turing, « Théorie des nombres calculables, suivie d’une application au problème de la décision », in La machine de Turing, Alan Turing, Jean-Yves Girard, Seuil, 1995, p. 52
mot(s)-clé(s) : Alan Turing, Hilbert, Kurt Gödel, machine de Turing
You can leave a response, or trackback from your own site.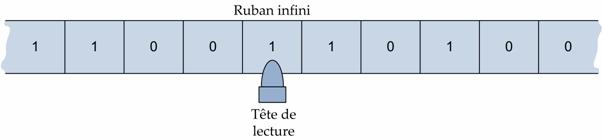
[...] Vincent LE CORRE – Psychologue – Psychanalyste − Alan Turing, sur les traces de l… Autour de #Turing, la #machine de Turing, première partie : http://t.co/MfcU2Tpy... Source: vincent-le-corre.fr [...]
[...] quelconque. (Dans la machine de Turing [lire le commentaire de l'article de 1936 de Turing première partie] inspiré de la machine à écrire, ce sera le ruban découpé en cases contenant des symboles à [...]
[...] travail effectué par l’humain devient fidèle à son concept de machine, dont nous avons parlé dans l’épisode 8. La machine est ce dispositif à deux propriétés principales : 1) une machine n’a effectivement [...]
[...] Alan Turing, sur les traces de l’IA : Episode 8 – la machine de Turing, première partie [...]